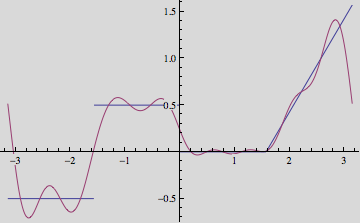Fourier Series Illustrations
William O. Bray
Our purpose here is to examine computation of Fourier sine and cosine coefficients and illustrate the pointwise convergence theorem.
All output has been deleted; so enter each Input Cell (white background) and hit Shift+Enter.
Computing Fourier Coefficients
Here are a couple of simple functions defined on the interval [0,π].
In[1]:=
![]()
Computing the Fourier sine coefficients is easy. For example
In[3]:=
![]()
Out[3]=
![]()
gives a formula for the Fourier sine coefficients of g. For plotting purposes, I find it useful to form tables of such coefficients for a range of the index n. I have also included the code to form the partial sums of the series and for the even and odd extensions of a function.
In[4]:=

Sine and Cosine Series for g
For example the following generates the first 20 Fourier cosine coefficients of g.
In[10]:=
![]()
Out[10]=
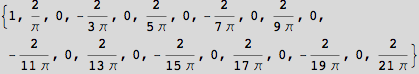
We can look at the numeric values with the command:
In[11]:=
![]()
Out[11]=
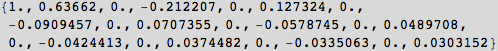
The plot of the function along with some partial sums is given as follows.
In[12]:=

Out[12]=
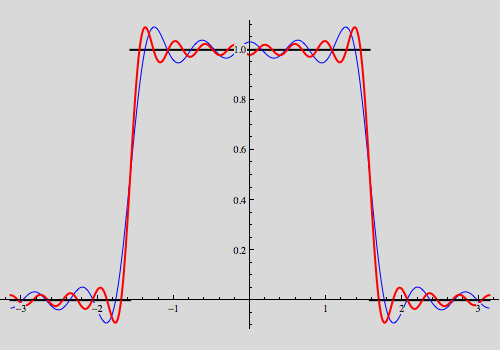
For the sine series, the commands are similar as follows. In both instances note the behaviour of the partial sums near the jump discontinuity; the Gibbs effect is apparent.
In[13]:=
![]()
Out[13]=

In[14]:=

Out[14]=
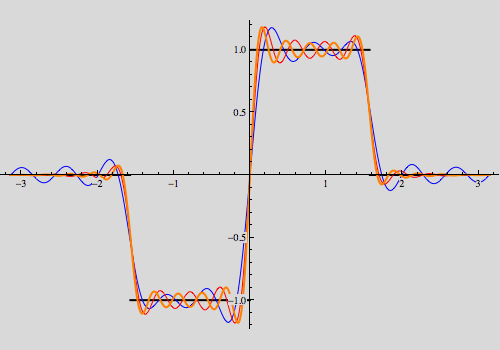
To illustrate convergence of the partial sums more dynamically, the following code does the trick
Fourier Sine and Cosine Series of gg
The following code presents similar computations and graphical illustration for the function gg.
In[17]:=
![]()
Out[17]=

In[18]:=

Out[18]=
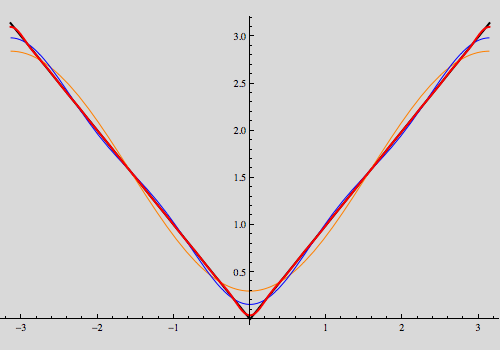
The above plot illustrates uniform convergence of the partial sums to the function.
In[19]:=
![]()
Out[19]=
![]()
In[20]:=

Out[20]=
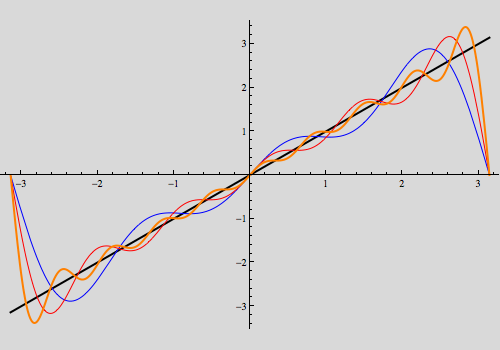
A non-piecewise continuous function
In[21]:=
![]()
This function is continuous everywhere on the interval [0,π] except at the point x=0. The Fourier cosine coefficients are given by (here the built in command for the coefficients is used; see the documentation):
In[22]:=
![]()
Out[22]=
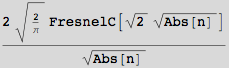
This may cause a "What???" in your mind. The expression on the right is one of the many special functions out there and is known as the Fresnel Cosine integral (see the Documentation Center for a definition). It originally occured in various optics problems.
None the less, we can capture the numerical values and plot the results as follows. This is followed by the same computations for the sine series.
In[23]:=
![]()
Out[23]=
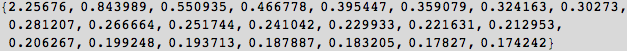
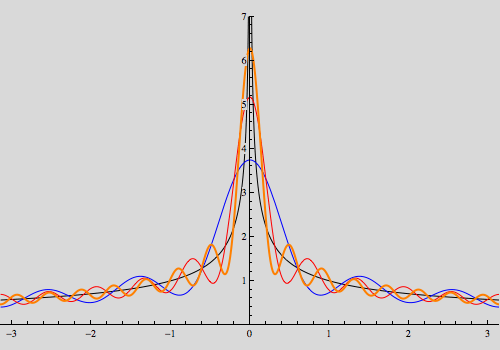
In[24]:=

Out[24]=
In[25]:=
![]()
Out[25]=
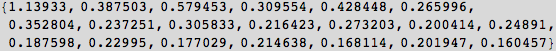
In[26]:=

Out[26]=
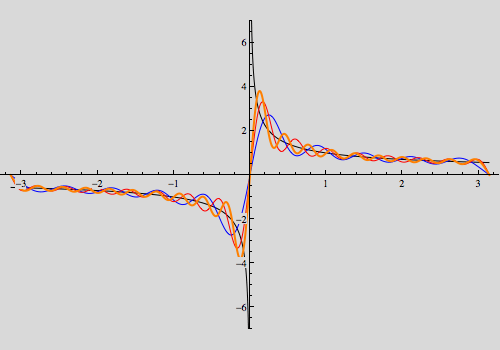
Both plots indicate that the Fourier sine and cosine series of h(x) does indeed converge to the function and in fact blow up at the singular point of h, facts we will not prove but are nonetheless, true.
Built in Functions
With the introduction of Mathematica 8, a variety of Fourier series functions are now built in. Here is one example, others can be seen in the documentation.
In[27]:=
![]()
Out[28]=
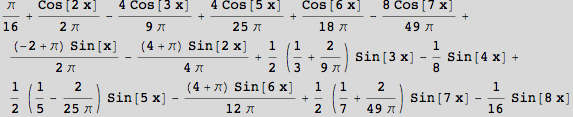
In[29]:=
![]()
Out[29]=