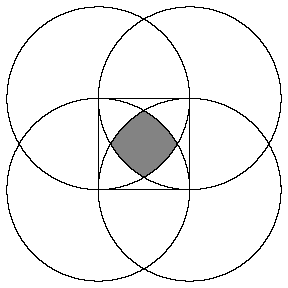

In the figure, four circles of radius 1 are placed with their centers at the vertices of a unit square. Find the area of the shaded region where they all overlap.

The main problem this month is to generalize the previous problem to three
dimensions. If eight spheres of radius 1 are placed with their centers at
the vertices of a unit cube, what is the volume of the region where they
all overlap?