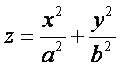

This year, the Missouri Collegiate Mathematics Competition will be held on April 17 and 18 here at Missouri State. This month's problem is a 3-dimensional version of an MCMC question from 1998 (click here to see an archive of old problems).
Given a point P other than (0,0,0) on the paraboloid whose equation is
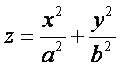
the normal line at P (i.e. the line perpendicular to the tangent plane at P) will meet the paraboloid at a second point Q. What is the minimum possible length of segment PQ?