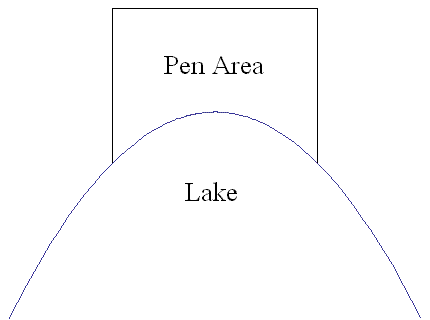

A farmer wishes to build a pen for his (non-swimming) animals next to a lake as shown in the figure below. The lakeshore has the shape of the parabola y = −x2. Two sides of the pen are parallel to the axis of the parabola and the third side is perpendicular to it. If the farmer has d units of fencing, what dimensions of the pen will maximize the area of the land bounded by the fence and the lake?
