
This month's problem has three parts.
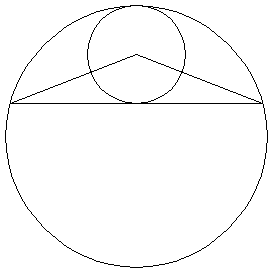
A circle of radius r is internally tangent to a unit circle. A triangle is formed by drawing a tangent line to the smaller circle that is parallel to the common tangent to the smaller circle and the unit circle and then joining each point of intersection of tangent line and the unit circle to the center of the smaller circle as shown in the figure below. Find the maximum possible area of the triangle.
Source: Gerhardt Hinkle

If we draw the analogous figure in space (namely rotate the figure above around the line through the centers of the circles), the circles become spheres and the triangle becomes a cone. What is the maximum possible volume of the cone? What is the maximum possible (total) surface area of the cone? For the latter, an approximate answer will suffice.
