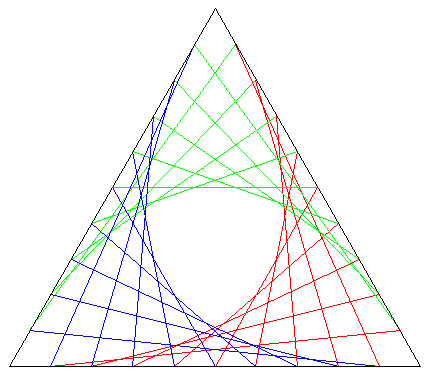

The figure below is inspired by a logo used to promote inclusiveness here at Missouri State University.

The figure is created by taking an equilateral triangle, placing points on each side of the triangle so that each side is divided into n = 10 congruent subintervals and connecting two points on adjacent sides with a line segment if the distance from one point to the common vertex plus the distance from the other point to that vertex equals the side-length of the triangle.
If we take the limit as n goes to infinity, we obtain the three curves shown below.
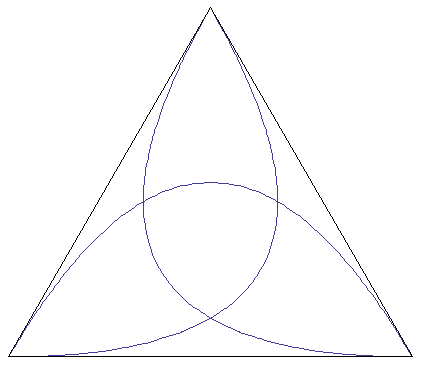
This month's problem is to compute the fraction of the area of the triangle in each of the resulting seven regions.
The solution will be posted shortly.

Back to the Advanced Problem Archives