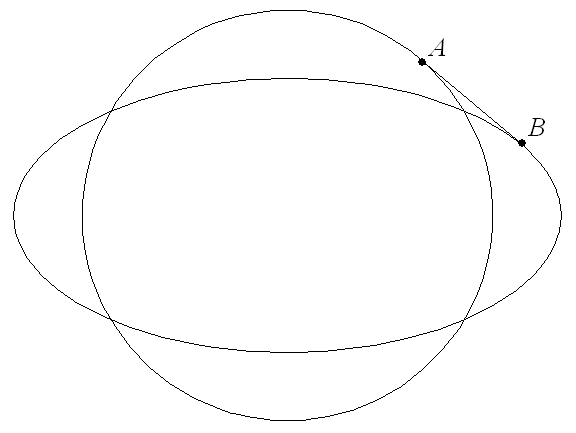

You are given a fixed ellipse with equation x2/a2 + y2/b2 = 1 and a varying circle with equation x2 + y2 = r2. Let A be a point on the circle and B be a point on the ellipse such that the line through A and B is a common tangent to the circle and to the ellipse (see figure below).
What is the maximum length of AB?

Source: K.R.S. Kastry
The solution will be posted shortly.

Back to the Advanced Problem Archives