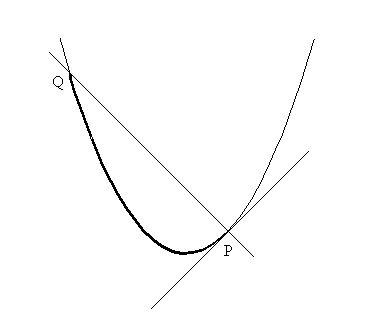

Let P be a point on the parabola y = x2 other than the origin, (0,0). The normal line to the parabola at P will intersect the parabola at another point, say Q. Find the coordinates of P so that the arclength along the parabola between P and Q is a minimum.
