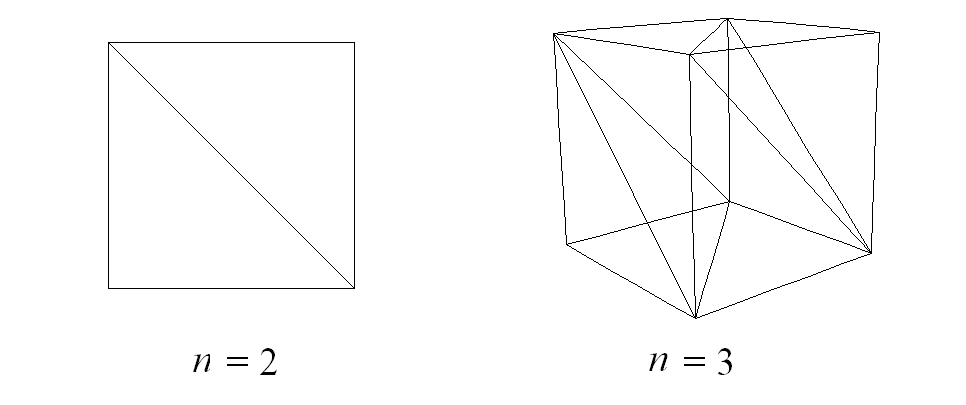

An n-dimensional hypercube is the convex hull of the 2n points (x1, x1, ..., xn), where the xi are 0 or 1. The hyperplanes x1 + x1 + ... + xn = k, k = 1,2, ..., n − 1 divide the hypercube into n pieces. Find the hypervolume of each piece.
For example, when n=2 we have a square divided into two isosceles right triangles each of area 1/2. When n=3 we have a cube divided into two pyramids and an octahedron. The pyramids each have volume 1/6 and the octahedron has volume 2/3.

The solution will be posted shortly.

Back to the Advanced Problem Archives