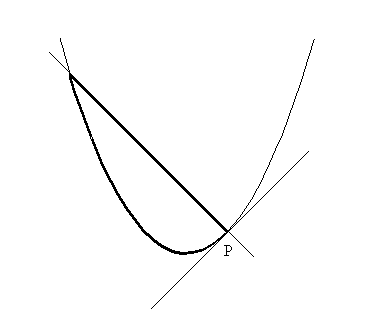

Let P be a point on the parabola y = x2 other than the origin, (0,0). The parabola and the normal line to the parabola at P will determine a bounded region. Find the coordinates of P so that the total perimeter of the bounded region is a minimum.
Note: You may give your answer numerically (say to five decimal places).
