Problem #35

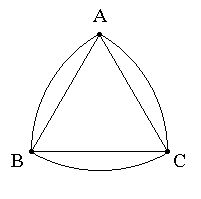
A Reuleaux triangle is constructed by taking an equilateral
triangle ABC and drawing the three circular arcs: BC with
center A, AC with center B, and AB with
center C, as shown below. The Reuleaux triangle is an example of a
"curve of constant width".
 This month's problem is to find the volume and the surface area of the
solid obtained by rotating the Reuleaux triangle shown above around a
vertical axis passing through vertex A. Express your answer in
terms of r, the length of a side of the original equilateral
triangle.
This month's problem is to find the volume and the surface area of the
solid obtained by rotating the Reuleaux triangle shown above around a
vertical axis passing through vertex A. Express your answer in
terms of r, the length of a side of the original equilateral
triangle.


