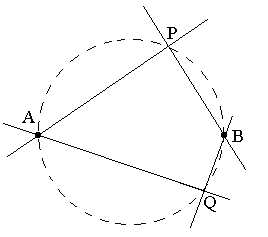

Consider a point in the plane that has two perpendicular lines through it that pass through two given points. In the figure below, A and B are the given points and P and Q are points such that angle APB and angle AQB are right angles. It is well-known that the set of all such points is a circle with the segment between the two given points as diameter.

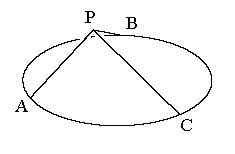
Consider a point in space that has three mutually perpendicular lines through it that each pass through the circle x2 + y2 = 1 in the xy-plane. In the figure below, A, B, and C are points on the circle and angles APB, APC, and BPC are all right angles. Find the locus of all such points P.