

Missouri State University's
Advanced Problem Page

© 1998, R. Mäder

|

|
Missouri State University's
|
|

|
Rhombicosadodecahedron © 1998, R. Mäder |
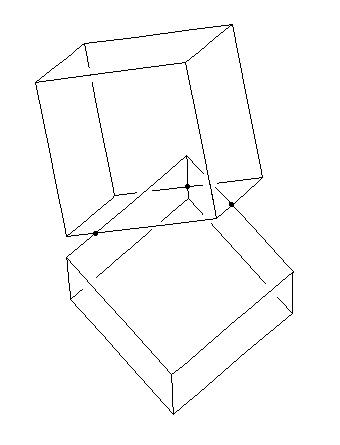
Consider two wire frame cubes having sides of length 1. As one cube moves towards the other, the interiors of the cubes will overlap, but at some point the edges of the cube will meet and the cubes will have to be rotated to make further progress. What is the furthest a vertex of one cube can get into the interior of the other, namely what is the greatest distance from the vertex to the face of the cube that is penetrated? An example of one cube interpenetrating another is shown below (the dots indicate points where the edges of the cube meet).
 Submit a solution
Submit a solution

Go to the Advanced Problem Archive
Back to the Math Department Homepage
Back to the Problem Corner
This page is maintained by Les Reid. Last updated January 8, 2015.