Solution to Problem #27
- If we denote the radius of one of the circles by r, then the
length of a side of the larger square is 4r. Denote the length of a
side of the smaller square by x. The distance from the center of
the larger square to one of the corners is 2*Sqrt[2]*r by the
Pythagorean Theorem. On the other hand, it is x/2 + 2r +
x/2 = 2r + x. Therefore, x = (2*Sqrt[2] -
2)r. The ratio of the areas is ((2*Sqrt[2] -
2)r)2/(4r)2 = ((Sqrt[2] -
1)/2)2 = (3 - 2*Sqrt[2])/2 or approximately .04289....
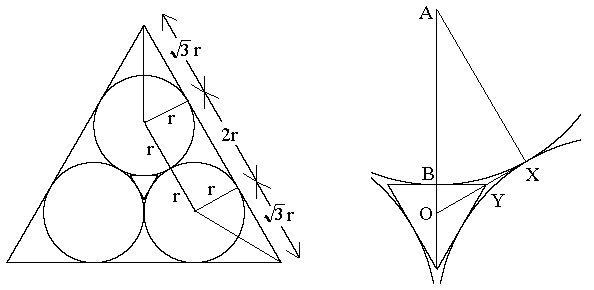
- If we denote the radius of one of the circles by r, then the
length of a side of the larger triangle is (2*Sqrt[3]+2)r [see the
first figure]. Denote the length of a side of the smaller triangle by
x. Consider the second figure, which is a blown up version of the
first. We have the measure of angle AOX = Pi/2 and AB =
AX = r, so AO = 2*Sqrt[3]*AX/3 =
2*Sqrt[3]*r. Therefore OB = (2*Sqrt[3]/3 - 1)r.
Since the measure of angle BOY = Pi/3, we have x/2 =
BY = Sqrt[3]*OB = Sqrt[3](2*Sqrt[3]/3 - 1)r and hence
x = (4 - 2*Sqrt[3])r. Since the ratio of the areas of the
triangles is the square of the ratio of the sides, we have ((4 -
2*Sqrt[3])/(2*Sqrt[3] + 2))2 = (26 - 15*Sqrt[3])/2 or
approximately .009619... as the ratio of the areas.
- An argument analogous to the one above show that a side of the larger
n-gon has length (2 + 2*Tan[Pi/n])r. The segment
analogous to OB has length (Csc[Pi/n - 1)r and hence
a side of the smaller n-gon has length
Tan[Pi/n]*(Csc[Pi/n - 1)r. After simplifying, the
ratio of the lengths of the sides of the n-gons is (1 -
Sin[Pi/n])/(Cos[Pi/n] + Sin[Pi/n]), so the ratio of
the areas is ((1 - Sin[Pi/n])/(Cos[Pi/n] +
Sin[Pi/n])2.
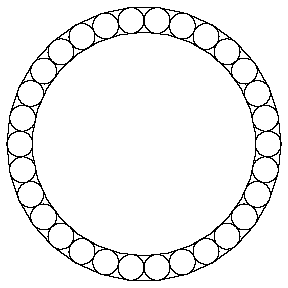
- The limit as n approaches infinity of the ratio above is ((1 -
0)/(1 + 0))2 = 1. This gibes with our intuition, since
as n gets larger, the smaller n-gon gets closer and closer
to the larger one. The figure shows the case when n = 30.