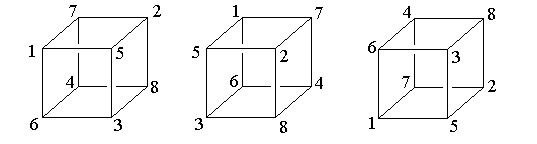

Up to rotation and reflection, how many ways are there to number the vertices of a cube using the integers from 1 to 8 such that no consecutive integers are connected via an edge of the cube? For example, one such numbering is shown on the left below. The two other numberings are equivalent to it (and hence would not be counted as distinct). The middle one is obtained by rotating the original 90 degrees around a vertical axis and the rightmost one is obtained by reflecting across a horizontal plane.
