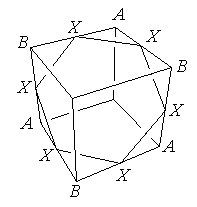

In the figure shown, the points labeled X are the midpoints of the segments with endpoints A and B. The X's all lie in a plane (the hexagon in the figure) and that plane divides the cube into two pieces of equal volume.
If instead the X's are chosen so that AX/AB = λ, determine what fraction of the volume of the cube lies on the same side of the plane containing the X's as the vertex that is adjacent to the points labeled A. For example when λ = 1/2, we are in our original situation and the fraction is 1/2. When λ = 0, the fraction is 1/6 (the corresponding piece of the cube being a pyramid).
