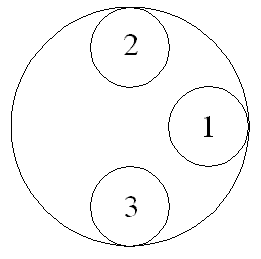

Two children play a game with three coins each having a radius of 1 unit. Each turn of the game consists of sliding one coin between the other two (without moving either of them). A given coin may not be moved in two consecutive turns. What is the smallest circular region in which it is possible for the game to be played indefinitely? For example, in the circular region shown below, coin 1 can be slid between coins 2 and 3, but then neither coin 2 nor coin 3 can then be slid between the other two.

Source: John Overdeck
Note: No correct solutions have been submitted to date.