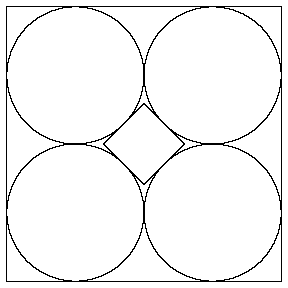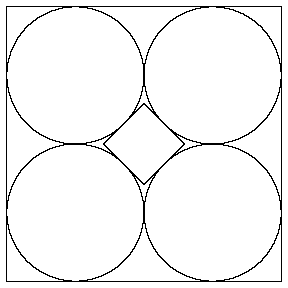Problem #27

This month’s problem has four parts:
- Four circles of the same radius are inscribed in a square as shown in
the figure. A second, smaller square is tangent to all four circles.
What is the ratio of the area of the smaller square to the area of the
larger square?
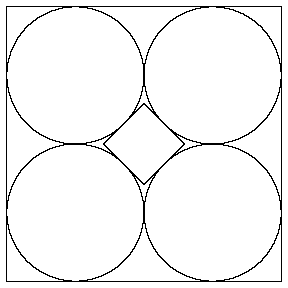
- Three circles of the same radius are inscribed in an equilateral
triangle as shown in the figure. A second, smaller equilateral
triangle is tangent to all three circles. What is the ratio of the area
of the smaller triangle to the area of the larger triangle?

- Generalize to an arbitrary regular n-gon.
- As n gets larger and larger, what happens to the ratio? Does
this gibe with your intuition?