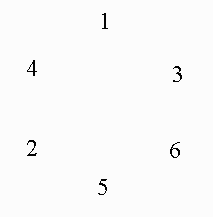

The integers 1,2,3,...,n (n > 2) are arranged in a circle in some order. How should they be arranged so that the sum of the products of all consecutive pairs is maximized?
For example, if the numbers are arranged as shown in the figure, the sum of the products of consecutive pairs is 1x3 + 3x6 + 6x5 + 5x2 + 2x4 + 4x1 = 73, but this can be improved upon.
Second, can you find a formula for the maximum value of the sum in terms of n?
What if you are to minimize the sum?