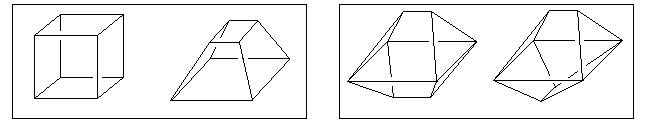

It is fairly easy to show that for any convex polyhedron, there must be at least two polygonal faces with the same number of sides. This month's problem is to find all polyhedra (up to "combinatorial type") such that no three faces have the same number of sides.
Roughly speaking, two polyhedra have the same combinatorial type if one can be deformed to the other. For example, a cube and a truncated square pyramid (shown below at left) have the same combinatorial type, but the two polyhedra shown at right do not. [Although they both consist of 4 triangular faces and 4 quadrilateral faces, a triangular face in the left-most polyhedron is adjacent to two quadrilaterals and one triangle, while a triangular face in the right-most polyhedron is adjacent to three quadrilaterals.]
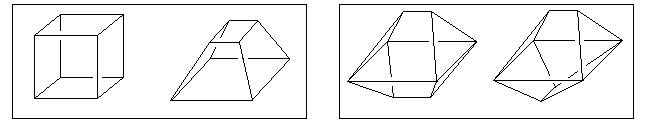
The solution will be posted shortly.

Back to the Archives