Problem #1

Consider tilings of a 1×n rectangle by a (possibly disconnected) tile
consisting of unit squares.
-
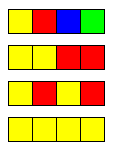
Suppose all of the tiles must be a translates of one another. For example, there
are four such tilings of a 1×4 rectangle as shown below (each tile is colored
a single color). The first tiling
has four unit tiles, the second has two connected tiles, the third has two disconnected
tiles, and the last has a single tile.
How many such tilings are there of a 1×12 rectangle?
Source: Harvard-MIT Mathematics Tournament
-
Can you determine a formula for the number of such tilings of a 1×n
rectangle?
-
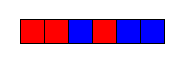
Suppose we allow the tiles to be translates or reflections of one another.
Such a tiling of a 1×6 tile is given below. Tilings that are reflections
of one another are to be considered distinct.
How many of these tilings are there of a 1×12 rectangle?
-
Can you determine a formula for the number of these tilings of a 1×n
rectangle?
The solution will be posted shortly.

Back to the Archives
Back to the Math Department Homepage.





