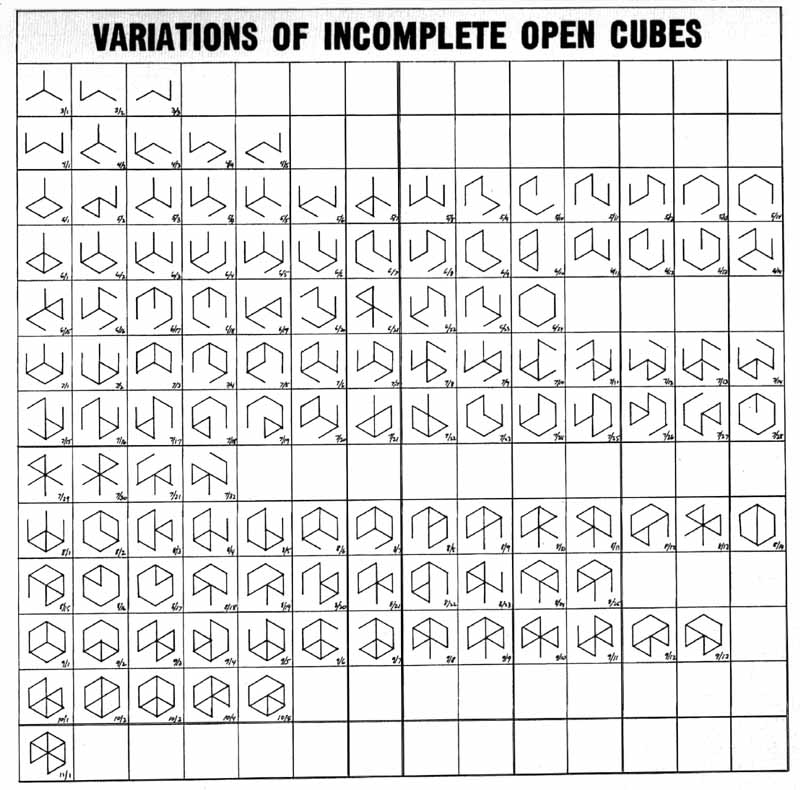

The conceptual artist Sol Lewitt (1928-2007) created a series of structures titled "Incomplete Open Cubes." They consisted of subsets of the twelve edges of a cube having the following properties:
Lewitt made both 2-D schematic diagrams and 3-D sculptures of the structures (see below), finding that there were a total of 122 such structures.
Here is a list of all of the schematics

and here is one of the sculptures (corresponding to the 12th entry in the 6th row of schematics).

This month's problem is to find the number of such structures for the remaining platonic solids (tetrahedron, octahedron, dodecahedron, and icosahedron).
The solution will be posted shortly.

Back to the Archives