Problem #1

This month's problem involves bracing figures rigidly using rods of
unit length.
1. An unbraced square is not rigid (see figure 1). If we are allowed to
build three-dimensional structures, we can brace the square rigidly using
an octahedron [two square pyramids back-to-back] (as shown in figure
2).
Find a way of bracing a square (with the minimal number of unit rods)
in the plane. [Note: In these problems, rods are only to be joined at
their ends.]
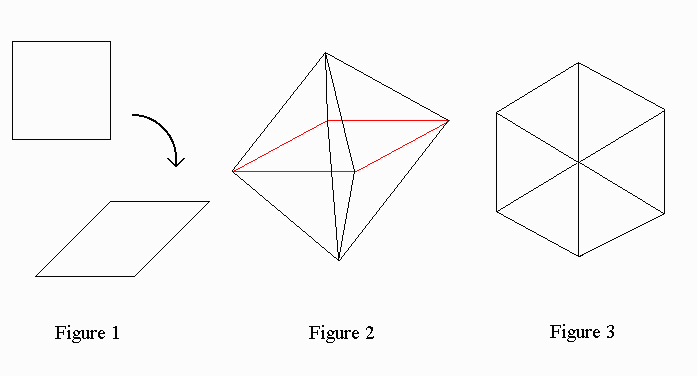
2. It's easy to brace a regular hexagon in the plane (see figure 3), but
this structure is not rigid in three dimensions. Find a way of bracing the
regular hexagon (with a minimal number of unit rods) in three
dimensions.
3. Can you brace a regular pentagon with unit rods in the plane? [This is
significantly more difficult than the first two questions.]


