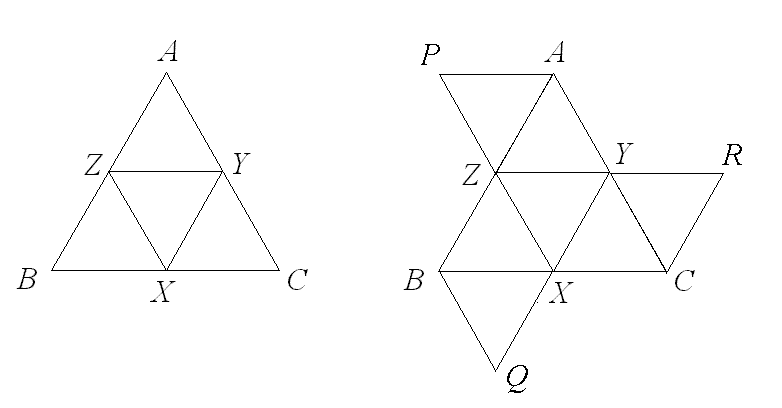

One can fold both of the triangular nets below to form regular tetrahedra. For the figure on the left, this can be done by identifying vertices A, B, and C. For the figure on the right, in addition to the previous identifications, we identify P with X, Q with Y, and R with Z. Note that in the second tetrahedron, some faces consist of two triangles from the net (e.g. APZ and BXZ). We define an edge of a tetrahedron constructed from a net to be open if it has no corresponding edge in the interior of the net. The first tetrahedron has three "open" edges (where AZ and BZ meet, where AY and CY meet, and where BX and CX meet), but the second has none.
Source: Charles W. Trigg
No solutions have been submitted.

Back to the Archives