Problem #3

An ant is placed on a 2 x 3 grid at the position marked X in the figure below. The ant moves along the edges of the grid as follows: from an intersection it randomly chooses one of the edges emanating from that intersection and moves along it, arriving at the next intersection one "step" later. [Note that under these rules, the ant is allowed to immediately double back on its path.] The points marked A and B are exits. When the ant gets to one of them it leaves the grid.

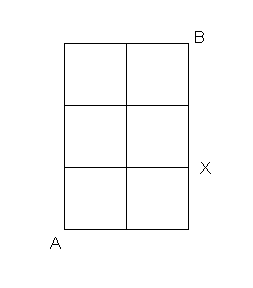
Is the ant more likely to exit through point A or point B?
On average, how long will it take the ant to exit the grid (either through point A or point B)?
If the ant is prohibited from immediately doubling back on its path, how does this affect the answers to the two previous questions?