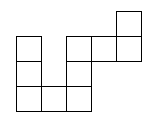

1. A 2-dimensional snake is a sequence of unit square in the plane, A(1), A(2), ..., A(n), such that
The figure below is an example of a 2-dimensional snake.
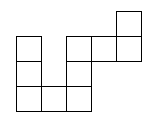
A 2-dimensional snake is said to be maximal if another square cannot be added to make a larger snake. This means that one can neither add a square A(0) nor a square A(n + 1). What is the smallest size of a maximal 2-dimensional snake?
2. A 3-dimensional snake is a sequence of unit cubes, A(1), A(2), ..., A(n), such that
A 3-dimensional snake is said to be maximal if another cube cannot be added to make a larger snake. What is the smallest size of a maximal 3-dimensional snake?
3. What about maximal snakes in higher dimensions?
The solution will be posted shortly.

Back to the Archives