
An m×n grid is filled with the integers from 1 to mn (inclusive) in any order. A marker is placed on the square containing 1. It is then moved to the square containing 2 via adjacent squares (squares sharing an edge) in the fewest moves possible. It is then moved to the square containing 3 under the same restrictions, etc. When it reaches the square containing mn it then returns to the square containing 1 (with the usual restrictions).
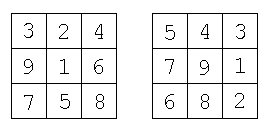
For example, when m = n = 3, a trip on the square on the left in the figure below, has stages of length 1, 1, 2, 3, 2, 3, 2, 3, 1 for a total of 18 steps. The square on the right has stages of length 1, 2, 1, 1, 2, 1, 2, 1, 1 for a total of 12 steps.

For given m and n, what is the shortest possible total trip length and what is the longest?
The solution will be posted shortly.

Back to the Archives