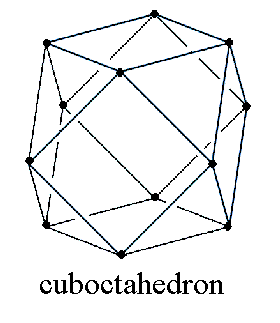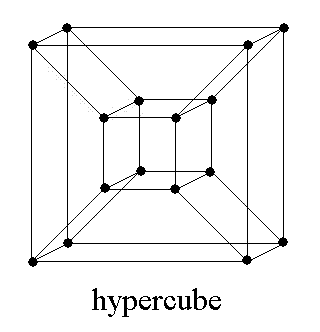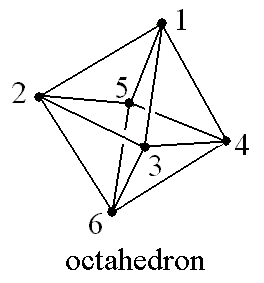

A graph is a collection of vertices and edges between them. A graph is said to have an euler circuit if there is a closed path on the graph that visits each edge exactly once. Euler proved that a graph has an euler circuit if and only if it is connected and every vertex has an even number of edges emanating from it. For example, the edges of an octahedron (see below) form a graph and every vertex has four edges emanating from it, so there must be an euler circuit and the sequence of vertices
gives one.

This month's problem asks: