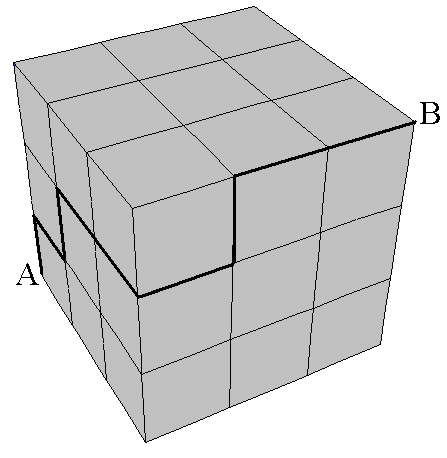

Given an n×n×n cube divided into n3 unit cubes if A and B are oppposite vertices, a legal path from A to B must be on the surface of the cube and be along line segments. One must always be getting closer to B (in other words, one can move up, but not down, right, but not left, and toward the viewer, but not away from the viewer).
A sample legal path is shown when n = 3. How many legal paths are there for an n×n×n cube?

The solution will be posted shortly.

Back to the Archives