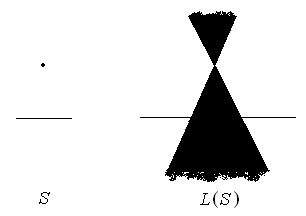

Given a set of points S, let L(S) be the set of all points lying on any line connecting two distinct points in S. For example if S is the disjoint union of a closed line segment and a point not lying on the line containing the segment, then L(S) consists of two vertical angles and their interiors and the line containing the segment as shown in the figure below. In this case, L(L(S)) is the entire plane.
This month's problem is to determine L(L(S)) when S consists of the vertices of a regular tetrahedron.

The solution will be posted shortly.

Back to the Archives