Problem #9

You are given four transformations of a 3×3 grid:

A takes the 2×2 square in the upper left-hand corner and rotates it 90 degrees clockwise.
B takes the 2×2 square in the upper right-hand corner and rotates it 90 degrees clockwise.
C takes the 2×2 square in the lower left-hand corner and rotates it 90 degrees clockwise.
D takes the 2×2 square in the lower right-hand corner and rotates it 90 degrees clockwise.

For example the result of performing transformation A followed by transformation D is shown below.

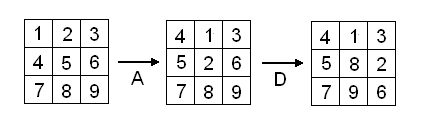
Show that begining with the grid numbered as above, any permutation of the numbers can be realized by a finite sequence of A's, B's, C's and D's.
Find the shortest possible sequence of such transformations that will switch the positions of "1" and "9" while leaving the remaining numbers fixed.
What is the least number n such that any permutation can be realized by a sequence of n or fewer transformations?