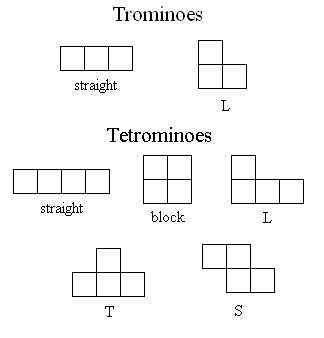


One wishes to color the standard tiling of the plane by unit squares so that any straight tromino (in whatever orientation) that is made up of tiles consists of three differently colored tiles. In this case, three colors is the minimum number possible and the coloring below realizes this minimum.

What if we have an L-tromino instead of a straight one?
What is the minimum number of colors required for the analogous problem for each of the tetrominoes (where we require that each tetromino consists of four differently colored tiles)?