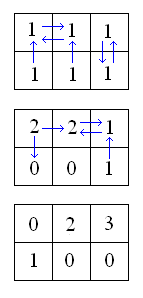

A marker is placed in each square of an m×n grid. One "turn" consists of each marker being moved to an adacent square (two squares are "adjacent" if they share an edge). Every marker must be moved. Markers in the same square may be moved to different adjacent squares. A configuration of markers will be represented by the number of markers in each square. A sequence of turns is illustrated below.

This month's problem is to determine how many configurations of markers can be realized by some sequence of turns on an m×n grid.
The solution will be posted shortly.