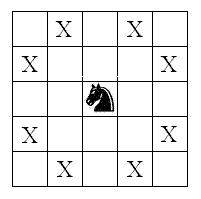

In chess, one knight move is two squares horizontally and one square vertically, or two squares vertically and one square horizontally. A knight can "jump over" any intervening pieces. In the figure below, the knight in the central square can attack all eight squares that are marked with an X.

This month's problem (which I have not yet determined the answer to) is:
"What is the maximum number of knights that can be placed on an n×n board so that each knight attacks exactly two other knights?"

For example, when n = 3 one can place 8 knights on the board so that each attacks exactly two others as shown in the figure above.