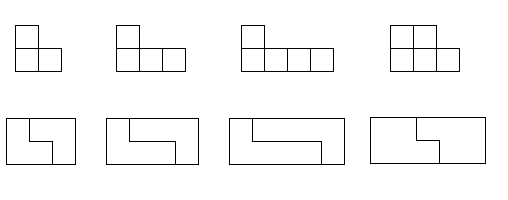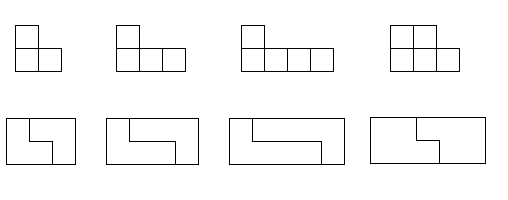Problem #12

The polyominoes shown below can each easily tile a square by combining two copies of the polyomino to form a rectangle as illustrated, then use these rectangles to tile a square.

• For each of these polyominoes, what is the smallest size square that can be tiled by the polyomino such that that tiling contains no smaller rectangle (of any size) that is tiled by the polyomino?

• Up to rotation and reflection, how many such tilings are there in each case?

The solution will be posted shortly.

Back to the Archives