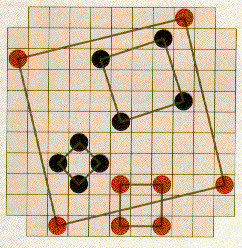
In the Mathematical Recreations column of the March 1996 issue of Scientific American, Ian Stewart describes a game played on an 11 x 11 board with the corners removed. The object is to place four markers on the corners of a square. The square may have edges that are parallel to the those of the board or may be tilted (see the figure below). Stewart states that "a huge number of possible squares can be formed". How many?