Problem #19

Consider all possible ways of coloring the squares of an n x n checkerboard
so that if n is even, the number of black squares equals the number of white
ones, and if n is odd, the number of black squares is one more than the
number of white ones. [Note that the standard checkerboard colorings
satisfy this condition.] Two colorings are considered to be equivalent
if one can be obtained from the other by rotation or reflection of the board.
For example, there are 2 inequivalent colorings of a 2 x 2 board (see figure).
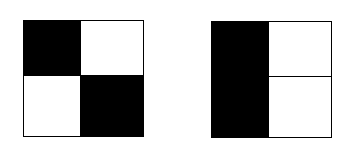
i. How many inequivalent colorings are there for a 3 x 3 board?
ii. For a 4 x 4 board?
iii. For an n x n board?


