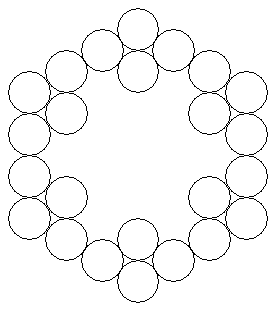
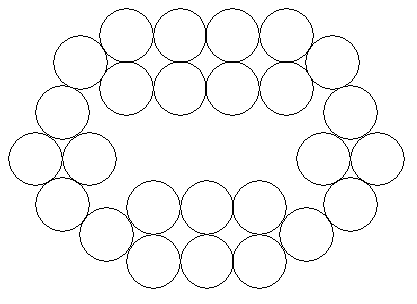
Ignacio Larrosa Cañestro of Coruña (Spain), John T. Robinson of Yorktown Heights NY, Jean Moreau de Saint-Martin of Paris (France), David Stigant, a teacher at DeBakey High School for the Health Professions in Houston TX, Dan Dima of Constanta (Romania), David W. Cantrell of Tuscaloosa AL, Yu Yat Hong of Singapore Polytechnic, and Ivy Fitzgerald of Chicago IL solved the problem under the (intended) interpretation that two circles were either tangent or did not intersect at all [Ross Millikan of San Mateo CA used a different interpretation, see below]. Most found the configuration below for 24 circles and used a graph-theoretical argument to show that there could be no such configuration for 25 (or in fact any odd number) of circles.

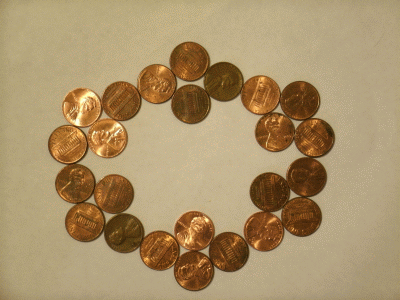
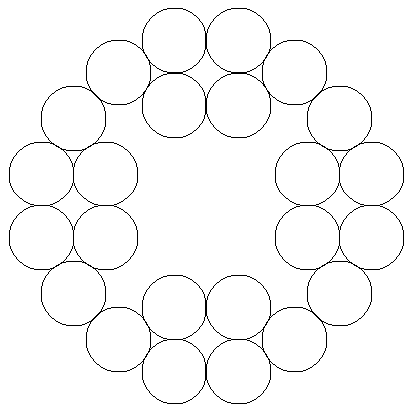
Yu Yat Hong also produced the configuration below.
This raises the question: How many combinatorially distinct configurations are there for 24 circles? One can use blocks similar to those of Hong (and of Stigant, see below) to produce other examples:
For what other number of coins can such a configuration be found? As indicated above, the number must be even. Dan Dima showed that this can be done for 4k coins. David Stigant extends this to any even number of coins greater than 14, leaving a few (probably negative) cases to be resolved. Here is David Stigant's solution:
Can you place 24 unit circles in the plane so that each circle is tangent to exactly three other circles? Yes. Arrange the circles in 6 groups of 4 on the vertices of a rhombus with 60 degree acute angles. Position the rhombi so that their long diagonals line up along the edges of a regular hexagon (as shown above). What about 25 unit circles? You cannot arrange 25 (or any odd number of unit circles) so that each circle is tangent to 3 others. Suppose you have an arrangement of circles with each tangent to three others. Let there be C circles and T points of tangency. Place a dot on either side of each point of tangency so that each dot is inside one of the circles which are tangent at that point. Each point of tangency will have 2 dots associated with it. Each circle with have 3 dots inside it. So there are 3C = 2T dots. Since the number of points of tangency must be an integer, C must be even. What about other (even) numbers of circles? The construction above for 24 circles can be adapted to any regular polygon except for a regular triangle. So any multiple of 4 greater than 12 can be arranged as desired. Also, it's possible to add 2 circles to one side of the polygon so that instead of rhombus on that side you have a "smushed" hexagon (see below). So any odd multiple of 2 (which is greater than 14) can be arranged as desired.That leaves 2, 4, 6, 8, 10, 12, and 14 circles. 2 circles won't work since you have to have at least 4 circles for any of the circles to be tangent to 3 others. 4 won't work. Each circle has to be tangent to all the others, so 3 of them must be arranged in an equilateral triangle. There's no way for the 4th circle to be tangent to all of the first 3. I don't have answers for 6-14, though I'm pretty sure 6 and 8 are impossible, and reasonably sure that the others are as well.
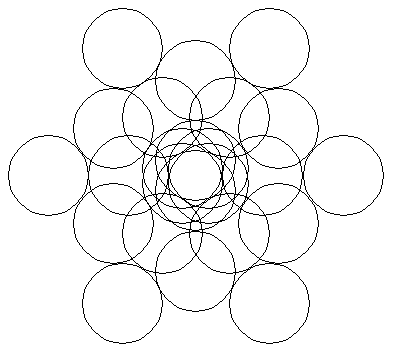
Ross Millikan allowed other intersection points. He noted that the generalized Petersen graph G(12,5) [the Nauru graph] with 24 vertices could be embedded in the plane as a unit distance graph [and no two non-adjacent vertices are unit distance apart]. He then dilated this by a factor of 2 and placed unit circles at each vertex to get the configuration below.