Bojan Basic of Novi Sad (Serbia) showed that there are 18 ways to cut a triangle with three cuts and found a lower bound (which he believes is sharp) of 136 ways to cut a triangle with four cuts. His solution is below.
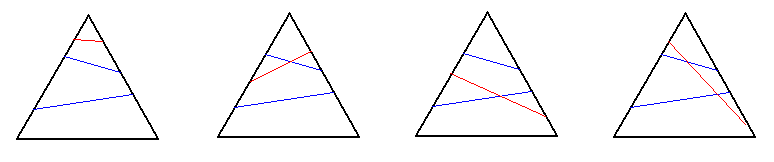
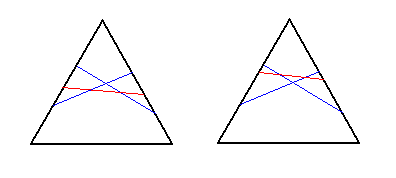
We will prove (by counting) that there are 18 essentially different ways of cutting a triangle with three cuts, and give a lower bound of 136 ways if four cuts are allowed. Three cuts: We shall follow the pictures from the statement, adding one cut to the each picture in all the possible ways (taking care of what's repeating). If we have two cuts which do not intersect, and if they connect the same pair of sides (as in the first picture): the third cut may also connect the same pair of sides, and in that case it can be added in 9 ways, 4 of which are essentially different; if the third cut connects one of these sides with the third one, it can be added in 3 ways, all of which are essentially different.


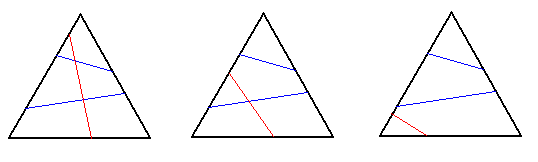
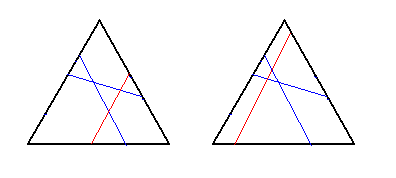
If we don't have the previous case, but we do have two cuts which do not intersect (as in the second picture): the third cut may connect the same pair of sides as one of the first two cuts already connects, and in that case it must intersects with it (in order to not repeat what was counted in the previous paragraph), which leaves only 2 essentially different ways; if the third cut connects the remaining pair of sides, it can be added in 3 different ways.
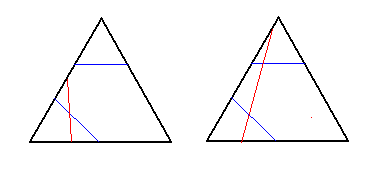
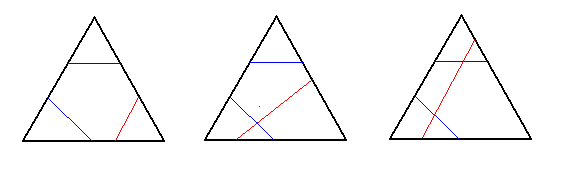
This leaves the case when all the cuts intersect. If all of them are connecting the same pair of sides (we are adding one cut to the third picture), that gives 2 ways; if all of them are connecting the different pairs of sides (we are adding one cut to the fourth picture), that gives 2 ways; if exactly two of them are connecting the same pair of sides (for example, the third picture again), that leaves 2 final ways.
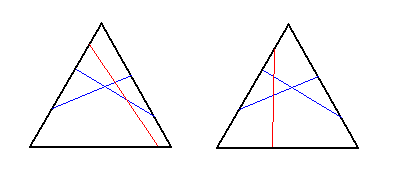
This makes a total of 18 ways. Four cuts: The lower bound for four cuts was found by computer, by randomly cutting the triangle, representing the picture as graph (with meeting points being the vertices, and the segments joining them being the edges), and checking how many non-isomorphic are among them. After about 40.000 tries, a total of 135 cuts was found, and it was standing still till about 55.000 tries (when the program was stopped). Checking the result showed that the cases with all four cuts connecting the same pair of sides were taking particularly long to be found, and then modifying the code in order to specifically search for only this kind of configuration found one more (which was found almost immediately, and lasted as the only one for about another 20.000 tries, when the program was stopped), making a total of 136. Of course, there is no guarantee that these are all of them (although this heuristic argument is pretty solid), but this indeed is a lower bound. The 136 graphs are here (as a 754 KB zipped file). For programming, Mathematica was used.