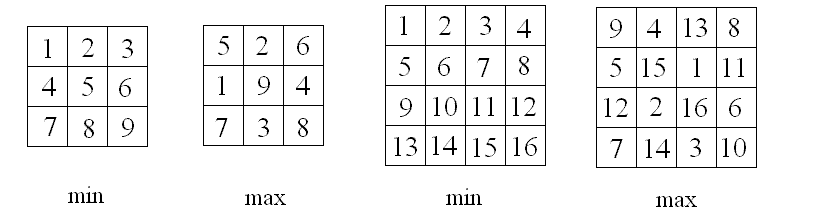
Paul Botham of Ipswich UK solved the problem and Claudio Baiocchi of Gavignano (Italy) generalized it. In the 3×3 case, the minimum is 24 and the maximum is 58. In the 4×4 case, the minimum was 60 and the maximum was 216. Examples are given below.

For the 2×2×2 cube, the minimum is 28 and the maximum is 48. Examples are given below.
For larger squares, the apparent minimum value (n3 − n) occurs for the array whose entries are in increasing order from left to right and up to down. Claudio Baiocchi's construction of a square having maximal value is given below. Using this construction, we find a maximum value of n4 − 4n2 + 8n − 11 for n odd and greater than 1 and n4 − 4n2 + 8n − 8 for n even.
Let us remark that an "optimal" solution should have the following property: the value inscribed in any square should be: GREATER or SMALLER than the values inscribed in ALL the adjacent squares and that this condition can easily be satisfied by the following strategy: working as in a chessboard, with White and Black cases, we put all the "big" values in the White cases and all the "small" values in the Black cases. (Or conversely; see later on.) Let us be more precise: call W4 the White squares having 4 adjacent squares (if any...); with similar definition for W3, W2 and (concerning Black squares) B4, B3, B2, we follow the scheme: - while free W4 squares do exist, put in one of them the biggest still unused value; then - while free B4 squares do exist, put in one of them the smallest still unused value; then - while free W3 squares do exist, put in one of them the biggest still unused value; then - while free B3 squares do exist, put in one of them the smallest still unused value; then - while free W2 squares do exist, put in one of them the biggest still unused value; then - while free B2 squares do exist, put in one of them the smallest still unused value. We have a lot of freedom but remark that the result is independent from the choices: the final result will be sum of 3 quantities, say: 4 * ( [the sum of the number on the W4 squares] - [the sum of the numbers on the B4 squares] ) 3 * ( [the sum of the number on the W3 squares] - [the sum of the numbers on the B3 squares] ) 2 * ( [the sum of the number on the W2 squares] - [the sum of the numbers on the B2 squares] ) and all these quantities are independent from the order and (also in a rectangular board, not only in a square one) easily evaluable. In particular: - on a 3X3 board (coloured with white center; but see later on) we put 9 in the center, 8,7,6,5 in the vertices and 1,2,3,4 on the remaining squares; for a total of 4*9-3*(1+2+3+4)+2*(5+6+7+8)=58. - on a 4X4 board (no matter the colouring) we hawe 4*(16+15-1-2) for the 4-adj squares; 3*(14+13+12+11-3-4-5-6) for the 3-adj squares; and 2(10+9-7-8) for the remaining squares; for a total of 4*2*14+3*4*8+2*2*2=8*(14+12+1)=216. Let us end with two remarks. REMARK 1 The 3-D case simply requires to replace "squares" with "cubes", paying attention to the fact that some further types (e.g. W6, B6) do exist. In the 2X2X2 case we simply have four W3 and four B3 cubes; our strategy brings to 3*(8+7+6+5-1-2-3-4)=48. REMARK 2 In a nXn square with even n, the reverse colouring gives rise to an identical number of W4, B4 and so on; thus the result remains unchanged. On the contrary, when n is odd, the reverse colouring exchanges the role of Black and White squares; but this simply replaces any value V with the value n^2+1-V. This does not affect the absolute value of the differences in adjacent squares and the total remains the same. Of course such a result would fail if the numbers to write into the squares are not the 1,...,n^2.