Solution to Problem #3

Ignacio Larrosa Cañestro of Coruña (Spain), Sudipta Das of Jadavpur University, West Bengal (India), Al Zimmermann of White Plains NY, Philippe Fondanaiche of Paris (France), Alexey Vorobyov of Irvine CA, Vince Lynch of Doncaster (UK), and Ross Millikan of San Mateo CA, solved the problem. Mathematical Induction was the most common method of solution. Here is Ignacio Larrosa Cañestro's solution:

Each equilateral triangle in the array is contained in a triangular array
T whose sides are parallel to those of the original array and the vertices
of the equilateral triangle lie on the sides of T. See the figure below.

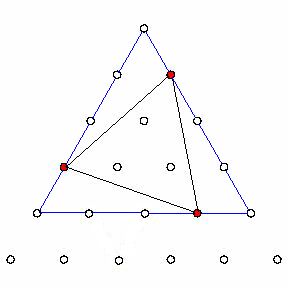
In the array there are Comb(k, 2)= 1+2+ .. + (k - 1) equilateral triangles
with (n-k+2) points on each one of its sides and the same orientation as
the complete array, for k=2 to n.

Taking a point on each side of a equilateral triangle, at the same distance
from the next vertex in clockwise order, we have an equilateral triangle.
Then, in a triangle with (n - k + 2) points on a side, we have (n-k+1)
equilateral triangles inscribed in it, including itself.

Then, the number of total of equilateral triangles in the array is:

Sum(Comb(k, 2)*(n-k+1), k, 2, n) =

Sum(Sum(Comb(i, 2), i, 2, k), k, 2, n)=

Sum(Comb(k, 3), k, 3, n +1)= Comb(n+2, 4)

In detail:

    Comb(2, 2) +

    Comb(2, 2) + Comb(3, 2) +

   .........

    Comb(2, 2) + Comb(3, 2) + ... + Comb(n-1, 2) +

    Comb(2, 2) + Comb(3, 2) + ... + Comb(n-1, 2) + Comb(n, 2) =


   Comb(3, 3) + Comb(4, 3) + ...+Comb(n, 3) + Comb(n+1, 3) = Comb(n+2, 4)



Comb(n + 2, 4) = (n^4 + 2n^3 - n^2 - 2n)/24

For n=1 to 10: 0, 1, 5, 15, 35, 70, 126, 210, 330, 495

Back to the Archives

Back to the Math Department Homepage.